Introduction
One of the aims of mathematics education is to develop higher order thinking skills in students. For centuries, teachers have been trying without success to accomplish this task, with the teacher-centered methodology. In recent years however, a more student-centered methodology has evolved and this has been seen as a means of developing high order thinking skills (Pehkonen, 1997).
Japan has a long history of successfully using open-ended problem to develop higher order thinking skills in students (Stevenson & Stigler1994). In 2012, a research was conducted in Japan to examine how expert teachers use open-ended problems to teach mathematics. The findings of the research led to the development of a framework that is intended to assist teachers as they guide students in solving open-ended problems in mathematics.
The purpose of this study is to present and discuss a framework for the use of open problems in mathematics classes, as practiced by two expert teachers in Japan.
Literature review
______________________* Correspondence:Lloyd Munroe, Hiroshima University, JapanEmail: kayanmunroe@gmail.comTeachers are students’ “guides” to academic achievement. Irrespective of geography, ethnicity or social status, the purpose of teaching remains the same: to produce intelligent, self-sufficient learners who are able to apply their knowledge to solve future problems and make valuable contribution to the society in which they live. Pedagogical methodology has been categorized as either teacher-centered or student-centered, with the latter deemed more appropriate for developing critical thinkers, self-sufficient learners, and problem solvers (Becker& Shimada, 1997; Hancock, Bray & Nason 2003; Cubukco 2012). In the teacher-centered approach, the student is a passive learner who tries to “absorb” and “reproduce” the prescribed body of knowledge presented by the teacher (Cubukco, 2012). In contrast, student-centered pedagogy focuses on students being active participants in the teaching – learning process. The student is in control of the pace and, in some cases, the content of their learning. “Student-Centered or “Learner-Centered” education has its origins in constructivist developmental theory (Piaget, 1948/1973; Fosnot & Perry, 2005). Constructivism refers to the idea that individuals “construct” their own understanding of the world as a product of their interactions with their environment. With respect to mathematics, rather than giving students a prescribed method of interpreting and calculating (as is seen in teacher-centered approaches), student are encouraged to apply their experience to solve routine and non-routine problems in their own unique way. The National Council of Teachers of Mathematics (NCTM), in the book “Principles and Standards for School Mathematics”, suggested that teachers should use a more student-centered approach in the teaching of mathematics.
The open-ended approach (Becker & Shimada, 1997) or open approach (Nohda, 1993) is a flexible, student-centered method which has recently gained popularity in the field of mathematics education. Here, students, working individually or in groups, are expected to apply their own unique methodology to solve given problems. These problems are so designed, that there may be more than one correct answer or there may be more than one way of arriving at an answer, thus they are able to challenge students at various levels of cognitive development. The problems used may be created from students` experience or by modifying regular classroom questions (Yee, 2002). Questions may also be created to satisfy the expectations or demands of the teacher.
Unlike in the usual teacher–centered approach this method eliminates the use of patterns, heuristics and generalizations, in solving problems. Here, the teacher facilitates and guides discussion and summarizes the lesson by recapitulating the strengths and weakness of each presented method (Becker et.al. 1990; Becker & Shimada, 1997; Pehkonen, 2004). Cooney et. al. (2004) suggested that students learn in different ways, and therefore, there is the need for a teaching method that will allow students to demonstrate their knowledge in a variety of ways. An open question is set so that students at various levels within the class can solve the problem based on his or her ability, experience and interpretation of the problem given.
A good open questions is difficult enough to challenge high performing students, yet simple enough so that the slowest member of the class can find at least one solution (Nohda, 1995; Yee, 2002; Kabiri & Smith, 2003). The use of open questions in the teaching of mathematics is promoted as they stimulate critical thinking, unearth idiosyncrasies in students, have practical applications to students` daily life.
Some teachers have difficulty implementing the Open Approach in the teaching of mathematics. Buschann (2004) mentioned that teachers complain about their inability to properly implement such an approach due to insufficient guidance on what to do and what to expect. Teachers are reluctant to administer open problems as they are afraid students may present solutions they cannot understand or that they may not be able to answer questions students may ask during discussions (Silver, Ghousseini, Gosen, Charalambous, & Strawhun, 2005). Teachers however, are not expected to be omniscient and therefore should not be embarrassed to seek help if necessary. Silver and his colleagues stated that 30% of teachers admitted in using open problems in the classroom and 20% of that 30% said they teach open problem as regular closed question with no in-depth discussions. The a lack of ability to control class discussions and insecurity in guiding students to develop higher order thinking, were reason given by teachers for not using open problems (Silver et. Al. 2005). Pehkonen (2008) stated that even teachers who are in favor of using the open approach still fail to implement it in their own class. These arguments give rise to the need for creating a guide that teachers can use, as they seek to implement the open approach.
The theoretical framework used in this study is based on the theory of constructivism and is aligned with the principles discussed in the book “The Open-Ended Approach: A New Proposal for Teaching Mathematics” by Becker and Shimada (1997). The book is based on the philosophy that each student can learn mathematics on the basis of his or her own experience, learning style, and stage of cognitive development.
Sekiguchi (2006) discussed mathematical norms in the classroom which create an environment in which students feel safe and comfortable to discuss and work with each other. He cited Yackel and Cobb, (1996) on their concept of ‘sociomathematical’ norms where the teacher creates a mathematics classroom that enhances and develops students’ mathematical thinking. The norms in the mathematics classroom involves promoting students’ growth by challenging them to think, justify, explain and find meaning in what they are learning (Stein and Smith, 1998). Fernandez (2005) in explaining Shulman’s Pedagogical Content Knowledge mentioned that the teacher should be able to understand the mathematics, understand how students think and that he should be aware of the different ways to further develop students thinking in order to help them overcome their difficulties.
Vygotsky’s Zone of Proximal Development (ZPD) is used to explain the difference between what students can do alone as against what they can do with assistance from others. The teachers’ ability to elicit information form students and help them to communicate their ideas, are therefore as valued as mathematical content knowledge itself.
Method
Two expert Japanese teachers, Mr. Hofu and Mr. Honda, (Pseudonyms) were observed using the open approach method with open-ended problems to teach mathematics to grade six students. Mr. Hofu was observed during the winter semester (October to February) and Mr. Honda was observed during the summer semester (April to July). In the fourth month of each observation, a class was selected for videotaping of a unit, subsequently, ten consecutive lessons were videotaped. These two classes, one with high performing students and the other with low performing students, were used as case studies. Towards the end of each semester, students were asked to complete a questionnaire about their views on learning with open-ended problems. A sample of students was selected for interview based on their responses to the questionnaire. The teacher was interviewed towards the end of the semester. The research focused on the teachers` actions before, during and after the lesson, as well as students` responses during and after each lesson. Data was collected through direct observations, transcript from videotaped lessons, questionnaires and interviews. Collected data from students were used as supporting evidence in developing the framework.
Participants
Mr. Hofu is in his early forties and has been teaching mathematics at the Elementary Level for over 20 years. He was invited to teach at the university-affiliated school due to his expertise as a teacher of mathematics. He is always mindful of the progression of the lesson and seems to be thinking one step ahead of his students. The open-ended problems used in his lessons required multiple solutions or multiple methods to obtain a solution.
Mr. Honda is in his late thirties and has been teaching mathematics at the Elementary Level for the past 17 years. He has a good command of the class as students listen and obey him when he speaks. He normally adapts questions from the textbook, which allow for the application of multiple methods to obtain one solution in his lessons.
A total of 176 grade six Japanese students between the ages of 11 to 13, from the selected schools, participated in the research. Students lived in the same city but were from different socio-economic backgrounds. Students were punctual, cooperative and prepared for each lesson. Each student had an attendance record of 90% or above, during the research period.
Data Analysis
The videotaped lessons were used as the main source of data as they were able to be repeatedly observed for in-depth analysis. It was as a result of this analysis that the framework for the use of the open approach was developed. The transcripts of the videotaped lessons along with the typed fieldnotes were organized into codes. The coding categories were devised based on suggestions by Bogan and Biklen (1982), and each code was broken down into sub-codes. It was generally observed that the teachers focused primarily on assisting students in understanding mathematical concepts and in applying their mathematical thinking. These headings were divided into five subheadings which were then cross analyzed with students’ responses and lesson development.
The Framework
The framework is called the Open Approach (OPA) framework and consists of two main sections, understanding mathematics and applying mathematics. Understanding was divided into ‘stimulate’ and ‘support’. Stimulate refers to eliciting information from students. Support refers to how the teacher guides students to explain their method(s) or solution (s). The Second section of applying mathematical thinking was further divided into ‘stretch’ and ‘strengthen’. Stretch refers to how the teacher guides students to apply the learned concept to the real world and strengthen refer to deepening students’ understanding in the mathematical world. The teachers provided continuous feedback to students and encouraged them to evaluate their own learning. This was observed when the teachers were supporting students in understanding and applying their knowledge, therefore the category of continuous evaluation was created. The word “successively” implies the constant mental assessment of students’ responses and adjustment of instruction performed by the teachers. A pictorial representation of the framework is shown in Figure1.

Figure 1. The open approach (OPA) framework
The framework was further developed by cross referencing the teacher’s action with students’ responses. Cross reference was looked at in terms of (1) the level of students’ participation, (2) how students got motivated and how they motivated others, (3) the different types and levels of questions used by both teachers and students, (4) the different levels of thinking displayed by students, (5) the progress of discussion and (6) the different types of solutions presented. Table 1 gives an overview of the cross reference analysis.
Table 1. Outline of the OPA framework
| Examples of categorized strategies in the open approach method | |||||
| The OPA Framework | Stimulate communication | Support conceptual understanding | Stretch math thinking to the real world. | Strengthen mathematical thinking | Successively evaluate |
| Participation | Stimulate and monitor students' levels of engagement. | Encourage students to ask for help when needed | Lessons flows from Individual to group learning. | Provide necessary information for students to solve the problem. | Maintain high expectations of ALL students |
| Motivation | Use students’ explanation for lesson content. | Remind Students of previously learnt problems with similar concepts | Use a variety of examples | Challenge students with information one grade above their level. | Write students’ names beside their solution |
| Table 1. Continued | |||||
| The OPA Framework | Stimulate communication | Support conceptual understanding | Stretch math thinking to the real world. | Strengthen mathematical thinking | Successively evaluate |
| Questioning | Encourage and assist students to ask questions | Use clarifying questions to guide students individually and in groups | Ask students about the reason behind their strategy. | Questions flow from peripheral to deeper thinking. | Consistently observe the functional grasp of ideas |
| Thinking | Give students time to think before responding | Asks a student to re-explain a peers' method. | Encourage students to think about the text and context. | Advocates for proof and accuracy | Encourage student to write their own summary |
| Discussion | Intermittently initiate class discourse during the lesson | Consistently refer to the concepts being taught. | Develop students’ reasoning skill | Encourage students to use math terms and symbols | Provide time for student to be reflective and critical |
| Solutions | Elicit many solutions or many methods from students | Encourage students to generalize and analyze concepts | Apply solutions to students' everyday life | Encourage students to use mathematical models | The board is used to capture the entire lesson. |
The horizontal headings show the connection between the vertical columns. The horizontal rows can be looked at as different sections in the lessons, i.e. introduction, development and summary but they can also transcend these sections. For example, the teacher motivates the students throughout the lesson.
Stimulate Communication
Stimulate and monitors students' levels of engagement. Teachers not only monitored students’ level of engaged but they encouraged, facilitated and acknowledged student’s input into class discussions. Some strategies that were common for both classes included (1) calling on different students to share their solutions to a question, (2) asking a student to repeat explanations given by his / her peer, and (3) asking one student to show a solution on the board then asking another to explain it. Mr. Hofu also allowed students to call on each other in giving solutions. He does this by posing an open-ended question and calling on one student to answer. The student gives an answer then calls on another student to answer, and the cycle continues.
Use students’ explanation for content of the lesson. One way of stimulating and motivating students to participate in the lesson was to use their own explanation for the content of the lesson. When students gave their explanation, the teacher echoed and wrote the statement on the board. These selected statements normally underlie a concept or fact, example, “zero times a number equal zero”. The teacher highlighted these statements whenever they emerged from other students’ explanation and discussion.
Encourage and assist students to ask questions. With the use of the scaffolding technique, Mr. Honda assisted students in asking questions during class presentation. First, he whispers a question to a student who repeats it aloud to the classmate making the presentation. Second, he begins the question or gives a hint as to what the students may ask. Finally, as does Mr. Hofu, he asks students if they had any question for the presenter. The teachers rarely answer questions posed to him by a student; instead, he passes the question on to the class and allows students to give their responses.
Give students time to think before responding. Thinking about a question before answering was common in both classes. The teacher asked a question, students paused and considered the questions for about 30 seconds, then raised their hands and waited for the teacher to acknowledge them. Occasionally, the teachers also allowed students to write down their answer(s) before raising their hands. Providing thinking time after asking a question was suggested by Shimada (1977) and Ontario (2006) as an important aspect in the development of student’s self-confidence and critical thinking skills.
Intermittently initiate classroom discourse and collaborative work. Both teachers initiated classroom discourse at various times throughout the lesson. Classroom discourse was used when students had opposing opinions, to provide extra time for students to discuss a mathematical premise and in situations where some students had difficulty understanding a statement. The teacher posed the question by highlighting the conflict, concept or misconception that he wants the class to discuss. He then gave instructions regarding the format of the discussion, that is whether in peers, small groups or as a whole class. Additionally, the teacher at times asks a student with an incorrect method or solution to show his work on the board. He then orchestrates a class discussion to help that student in identifying his error. This application of classroom discourse and collaborative work, according to the NCTM (1994) facilitates the development of new collaborative knowledge and further enhances students’ cognitive development.
Elicit many solutions or many methods from students. The teacher elicited many methods and solutions from the students by highlighting the openness of the questions. During students’ presentation, the teacher asked questions such as “Who did it another way?” or “Who has a different explanation?”. These questions stimulated students to challenge themselves in finding alternative ways to solve the problem, or to arrive at alternative solutions to the problem.
Support Students’ Conceptual Understanding
Encourages students to ask for help when needed. Both teachers reminded students to ask for help when need. During class discussion, after asking a question and giving students time to think, Mr. Honda sometimes asked students who have a solution to stand. Others, who thought that they needed help, are then allowed to go and ask one of those standing, for assistance. In the interview, when asked why he encouraged students to ask for help, Mr. Honda said, “students take more responsibility for their learning when they ask for help rather than when their peers volunteer to help them.” Asking for help is not a sign of weakness, but implies that the child recognizes his limitation and is willing to accept guidance to overcome that limitation.
Reminds students of previously learnt problems with similar concepts. Reminding students of past problem-solving situations was an effective strategy used by the teachers. Both teachers began their lessons by recapping what was done in the previous lesson. During seated work, when students are “stuck” on a problem, the teachers used questions to help them remember similar problems they did in past lessons. The teacher may asks “did you do anything yesterday similar to what you are trying to do now?” This helps the student to reflect on what was done and to use that information to assist him in solving the current problem. Students were allowed to read the notes from previous lessons if they forgot what was done.
Use clarifying questions to guide students individually and in groups. The teachers used open questions to guide students’ thinking. The data shows that of the 38 to 64 questions asked in a given lesson; 50% to 60% were clarifying questions. The teachers used words such as “so…”, “then…”, and “therefore...” to encourage the student to give more information or think more deeply about the concept.
Asks a student to re-explain a peers' method. One way of eliciting information from students and ensuring participation in the lesson was to ask a student to re-voice another student’s explanation. Both teachers practiced this in their lessons. Three reasons given for doing this were; (1) to confirm that the student understood what was said and (2) to elaborate or rephrase the explanation, and (3) to give student an opportunity to participate in the lesson, especially when both students used the same method to solve a problem. In doing this, students were motivated to listen to each other during classroom discussion.
Consistently refer to the concept(s) being taught. Some statements were consistently referred to throughout discussions in the lesson. These two or three statements were normally mathematics axioms or laws obtained from students’ explanation during discussion. The teacher consistently reminded students of these statements each time they were mentioned. For example, the statement “zero times a number gives zero” was repeated 11 times in 50 minutes by students and 18 times by Mr. Honda during the discussion of the lesson. Repetition promotes memory the concept while discussion provides in-depth understanding of the said concept.
Encourage students to generalize and analyze concepts. Many solutions were obtained from a given question. These solutions sometimes formed an easily identifiable pattern. Mr. Hofu encouraged his students to analyze these patterns and to try to make generalizations from them. In doing so, students created fixed premises on which to build their arguments. The students in Mr. Hofu’s class often tried to prove mathematical statements by using their own concepts and ideas.
Stretch mathematics thinking to the real world
Lessons flow from Individual to group learning. Students were given time to think about the problem by themselves. During this time the teacher moved about the class and purposefully and mentally recorded the various approaches used by students. He then asked different students in turn, to share their approach with the class.
Uses a variety of examples in explanation. Both teachers provided multiple ways of thinking about the problem. This was done to help students to think about different ways that the problem could be solved. Teachers sometimes facilitated an open discussion on the various ways in which the problem could be solved before giving the class the opportunity to solve it. This provided hints to slower student as to ways they could approach the question. Students were not forced to use any of the stated approaches and they often opted to use their own methodology.
Ask students about the reason behind their strategy. Mr. Hofu and Mr. Honda frequently question students about their reasons for using a particular approach. This form of questioning helped students to look beyond the calculations and to examine its application to real life. Students often revised their calculation to make them more efficient and applicable in the real world. For example, instead of adding a number seven times the student may resort to multiplying the number by seven.
Encourage students to think about the text and context of the question. In introducing the problem to the class, both teachers followed a pattern of asking students to read and re-read the problem statement, then they highlight words or phrases that may be difficult to understand. These were openly discussed. Finally, they asked two or three students to rephrase the problem in their own words.
Develop students’ reasoning skill. Students’ reasoning skill was developed during classroom discussions as they were able to see various ways of interpreting the problem. Through comparison and discussion with practical reasons students developed skills such as critical and analytical thinking. Both teachers impressed upon students the need to create a balance between defending their opinions with practical and convincing arguments and to relinquishing their position when the evidence was against them.
Apply solutions to students' everyday life. Both teachers encouraged students to observe the practical applications of their solution. In some lessons, discussed different ways in which the solution maybe applicable to students’ everyday life. Giving different ways of applying new knowledge helped students to think more widely about what they have learned. Students could therefore determine how to apply learned information to new and unfamiliar situations.
Strengthen mathematical thinking
Provide necessary information for students to solve the problem. First, the teachers questioned students about their understanding of the problem. They stressed important aspects in students’ responses as a means of providing hints regarding what they should consider when attempting to solve the problem. Second, the teachers reminded students of past problems that were similar; the students had the option of applying or modifying previously used method to solve the current problem, or to develop a totally new approach. Third, the teachers provided one to one assistance during individual work. This is referred to in Japan, as Kikan-shido. (See Munroe, 2015)
Challenge students with information one grade above their level. Students sometimes asked questions to which the answer would take them to more advanced mathematics. To this, the teacher would give a response such as, “You will encounter this mathematics when you are in grade 7 but I wonder who would like to try it now” Occasionally, the class agreed to explore the question. In cases where the group opted not to continue the discussion, the teacher made himself available to assist individual students who chose to attempt the question, after class or for homework.
Questions flow from peripheral to deeper mathematical thinking. The teachers led students deeper into mathematical thinking by increasing the difficulty of the questions posed. Class discussions often progressed to higher levels of thought as students are directed to focus emerging patterns or trends. The field notes showed that questions toward the beginning of the lesson were specific and concrete, but questions toward the end of the lesson were abstract and general. As students focused more on their calculations, different patterns emerged, the teachers questioned students about the relationship between these patterns which forced students to think about why these connections between concepts exits and how to manipulate them.
Advocate for proof and accuracy. The teachers tried to deepen students` mathematical reasoning by asking them to use previously established facts as reasons for their argument. It was common to hear statements such as, “We already know that…” or “It was shown that…..” or “Because we know that… we can determine…” in discussion. This also strengthened students` ability to critique each other`s method pertaining to reasons and efficiency of presented calculations and methods. In this manner students became familiar with the process of mathematical proof even without the teachers using the word “proof”.
Encourage students to use mathematical terms and symbols. Students were encouraged to use mathematical symbols instead of words when writing and to use mathematical terms in their explanation. Using the mathematical terms allowed students to become familiar with them. The teachers carefully listened to how students` use these terms and immediately corrected misuse when the need arose.
Aid students in focusing on necessary information and in using models. Students often had difficulty extracting necessary and relevant information required for the solution of a stated problem. In these cases, the teachers helped by highlighting the pertinent information needed to deepen mathematical thinking. One way they did this was by encouraging students to use models. For example, in one lesson, the class discussed how to find the total capacity of a bottle if 600ml is 2/3 its capacity. Some student drew actual bottle shape objects and other drew rectangular shaped models. Figure 2 shows the four different ways students drew bottles. The teacher pointed out that the shape of the bottle was not important for calculation and affirmed the student’s effort. Some students used the lines in their note books as guides to help them to divide their rectangular shape bottle into three equal three equal parts.
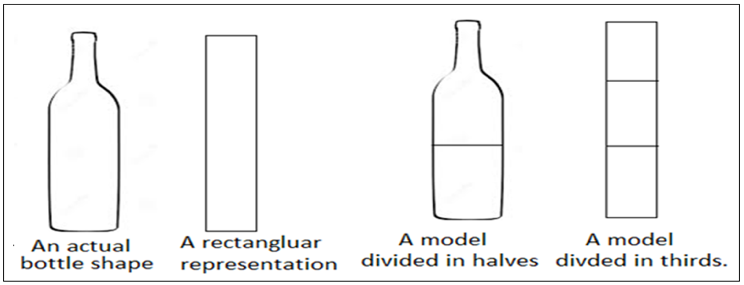
Figure 2. Different ways students drew models of a bottle to assist in their calculation of its volume
Successively Evaluate
Maintain high expectations for ALL students. All students were expected to attain the learning goal by participating in class activities and attempting to solve the given problem. Students did not complain about the difficulty of the problem nor their inability to solve it. Each made an attempt and each was willing to ask for help when it was needed. Japanese philosophy promotes the idea that regardless of the task, with hard work, each one can succeed. (Stevenson & Stigler, 1994).
Write students` names beside their solution. Students` name cards were placed beside their method or suggestions when these were recorded on the board. This served three main purposes; (1) it gave a sense of ownership and recognition for the method or suggestion, (2) it increased the self-worth of the student as a valued member of the class and (3) it assisted in discussion as students could direct their question to the person who gave the method or suggestion.
Consistently observe the functional grasp of ideas. The teachers focused more on how students grasped the functional use of concepts rather than the speed of obtaining the solution. During seated work, the teachers questioned students individually, to ensure that the student fully understood their chosen solution path. During class discussion the teachers listened keenly to both the questions asked and the solutions given. Along with correcting any misconceptions, the teachers also provided additional information to assist the presenter where necessary.
Encourage students to write their own summary. Toward the end of the lesson, after giving a verbal summary of the class discussions, the teachers encouraged the students to write a summary reflecting on what they learned. Students could include what they understood least, what the liked about the lesson, un-answered questions they may have, their opinion on the various methods presented in the lesson, how the knowledge gained related to other topics in mathematics and how they may apply what they learned. Students were free to choose what to reflect on and what to write. They could write a simple explanatory sentence or paragraphs. For example a student wrote in his reflection, “I liked my strategy but I think Taro’s (pseudonym) way was better so I will use his.”
Provide time for students to be reflective and critical. The teachers provided time for students to present their ideas and to critique ideas presented by others. This was done by initiating a discussion after each method was presented. During presentation, the class listened and observed as ideas were presented in a step by step format, with a mathematical rationale given for each step. The presenter remained at the board and waited for questions and suggestions from classmates.
The board is used to capture the entire lesson. The board was used to summarize the discussion and activities within the lesson. The teacher reflected on these ideas at the end of the class. The teachers wrote on the board being mindful of other information that may be useful for further discussion as the lesson progressed. They also directed students regarding where to write on the board. The board was never erased during the lesson. Additional mobile boards were used if necessary.
Conclusion
Both teachers established a friendly classroom atmosphere where students were free to share their opinions without being ridiculed. The goal of the class was to learn and students worked as a team to achieve this. Students were often heard encouraging their peers and being encouraged to do their best. Mistakes were seen simply as a sign of ignorance rather than as a sign of retardation. The teachers encouraged students to assist those who showed a lack of understanding. More advanced students were expected to assist those who were struggling. There was a high level of respect among the members of the class. These factors maybe underlining requirements for successful application of the OPA framework
